Matematika
5.ročník
Milí piataci , určite aj k Vám sa donieslo , že v školstve postupne prichádzajú zmeny . Na hodinách matematiky ste určite zistili, že pridávame nové metódy, hry a iné hodiny . V prípade ak by ste chceli rodičom ukázať, čo robíme alebo ak budete chýbať a chcete nájsť čo robíme a nestratiť ani jednu novú vec ponúkam Vám túto možnosť.
V dokumentoch nájdete opis prostredia z Hejného matematiky v ktorom sme sa učili matematické operácie alebo postupy poťítania.
Čo nás čaká v jesenných mesiacoch?
|
1. cieľ
september , október - 40 hodín
Pracovať s prirodzenými číslami, zlomkami, desatinnými číslami a s celými zápornými
číslami pri riešení úloh a problémov.
|
1. Rozširovanie oboru prirodzených čísel
Pojmy
Aktívne: zaokrúhľovanie, zaokrúhľovanie nahor a nadol, približne, presne.
Pasívne: rozklad čísel; rád číslice a čísla; opačné čísla; odhad, záporné a kladné celé číslo.
2. Základy práce so zlomkami
Pojmy Aktívne: zlomok, zlomková čiara, čitateľ, menovateľ.
3. Základy práce s desatinnými číslami
Pojmy Aktívne: desatinné číslo, desatinná čiarka, desatinné miesto.
|
|
2. cieľ
Analyzovať, opísať a uplatniť pravidlá vo vzoroch a postupnostiach a riešiť
praktické úlohy s využitím závislostí medzi veličinami alebo využitím vzťahov
medzi rôznymi jednotkami miery.
|
4. Číselné výrazy a jednoduché rovnice a nerovnice v riešení úloh
Pojmy
Aktívne: súčet, sčítanec, rozdiel, menšenec, menšiteľ; súčin, činiteľ, podiel, delenec,
deliteľ, zvyšok.
Pasívne: neúplný podiel, neznáma.
Závislosti, vzťahy a práca s údajmi
1. Práca so vzormi a postupnosťami
Pojmy
Aktívne: pravidlo.
Pasívne: vzor, postupnosť čísel.
2. Rozšírené nástroje na prácu so závislosťami a vzťahmi
Pojmy
Aktívne: súčet, rozdiel, súčin, podiel, "o _ viac/menej", "_‐krát viac/menej", "_násobok",
hmotnosť, gram, dekagram, kilogram, tona; objem, mililiter, deciliter, liter.
Pasívne: číselný výraz.
|
|
1 písomná práca
|
Témy: veľké čísla, porovnávanie, zaokrúhľovanie, rímske čísla, eurá, zlomky, sšítanie odčítanie, násobenie, delenie prevody jednotiek, Hejného rovnice
|
Prostredie
Krokovanie

Steppping je aktivita (hra), v ktorej sa rozvíja nielen schopnosť počítať, pretože toto prostredie je založené na rytme. Tu dieťa rozvíja schopnosť synchronizovať slovo a pohyb. Okrem toho sa dieťa učí sčítať, odčítať, rovnice a absolútnu hodnotu. Otvára sa tu svet záporných čísel.
Materská škola
Základom počítania je rytmus. Spievame a tlieskame do rytmu. Napríklad "Paci – paci – pačič – ky, – to – are – mine – ručič – ky".
Potom pridáme chôdzu. Rodičia skandujú a tlieskajú, dieťa kráča do rytmu. Ak existuje priateľ, obaja vykročia vpred. Na zem položíme šliapací pás a deti naň stúpia.
Keď sme dobrí v krokovaní, začíname s pridaním. Na začiatku pásma stoja Eva a Adam vedľa seba (v prípade núdze hrá jeho babička). Mama prikazuje: "Eva, dva kroky a potom jeden krok, začnite hneď!" Eva urobí krok, všetci tlieskajú a počítajú: "Jeden, dva. Jeden." Mama sa pýta, koľko krokov musí Adam urobiť, aby sa opäť postavil vedľa Evy. Dieťa povie "tri" a matka prikáže: "Adam, urob tri kroky, začni hneď!" Chlapec odíde, všetci sa počítajú a tlieskajú. Deti stoja vedľa seba, problém sme vyriešili.
Iné úlohy sú náročnejšie a potom prichádzajú kroky späť. Napríklad: "Eva, urob dva kroky vpred, potom jeden dozadu a potom dva dopredu."
Keď dieťa vykročí "jeden krok vpred, potom tri kroky dozadu a potom štyri vpred", začne budovať chápanie záporných čísel. Ak má dieťa záujem o krok, naše vyučovanie je úspešné.
1. a 2. ročník
Pokračujeme v čoraz náročnejších príkazoch. "Urobte päť krokov vpred, štyri kroky späť, dva kroky vpred, tri kroky späť, jeden krok späť, začnite teraz." Takýto príkaz je už veľmi komplikovaný. Študent si to musí zapísať. Zápisy žiakov budú odlišné a niekto objaví písmo pomocou šípok. Potom si zapíšeme dlhý príkaz.
| →→→→→ | ←←←← | →→ | ←←← | ← |
Eva dostane tento príkaz a my sa pýtame: "Aký jednoduchý príkaz mám dať Adamovi, aby opäť stál vedľa Evy?" Pomocou šípok to zapíšeme.
| →→→→→ | ←←←← | →→ | ←←← | ← | = 
Pomocou čísel napíšeme úlohu 5 – 4 + 2 – 3 – 1 = __.
Riešenie problému je | ← |, t. j. –1.
Podobne aj úloha | → | | ←← | = | →→ | Môžeme napísať 1 + __ – 2 = 2.
| ←← | = | →→ | Môžeme napísať 1 + __ – 2 = 2.
Jeho riešenie je | →→→ |, t. j. 3.
Úloha 1:
a) →→→→ | ←←← | = | |
|
b) →→→→ | | = | →→ |
| = | →→ |
c) → | | ←←← | = | →→ |
| ←←← | = | →→ |
d) →→→ | ←← | = | →→ | |
|
3. a 4. ročník
Pomocou počtu predmetov nemôžete získať záporné čísla. Úloha "Mám dve jablká, zjedol som tri, koľko mi zostáva?" je absurdná. Keď však úlohu preložíme do jazyka krokov, nevzniká žiadny problém.
Úloha má riešenie | →→ | ←←← | = | | Moje riešenie | ← |, teda –1. V algebre jazyk: 2 - 3 = x, takže x = –1.
| Moje riešenie | ← |, teda –1. V algebre jazyk: 2 - 3 = x, takže x = –1.
Krok umožňuje študentovi pochopiť záporné čísla. Dokonca aj náročný výraz "mínus pred zátvorkou". Rozumie sa to "smerom dozadu" (ČV = ↺).
Napríklad výraz 3 - (2 - 1) preložíme na šípky: | →→→ | ↺ | →→ | ← | ↺ |
Vhodný príkaz je: "Urobte tri kroky vpred, tvárou dozadu, dva kroky vpred, jeden krok späť, tvárou dozadu." Ak bol študent na začiatku otočený k dverám, urobí tri kroky k dverám, potom otočený dozadu, potom dva kroky od dverí, potom krok späť k dverám a nakoniec otočený späť (toto je koniec zátvorky). Teda, | →→→ | ↺ | →→ | ← | ↺ | = | →→ |
5. a 6. ročník
Ďalším náročným matematickým konceptom, ktorý možno ilustrovať krokom, je absolútna hodnota. Adam stojí na bežiacom páse, Eva o krok pred Adamom. Našou úlohou je dať im také príkazy, aby spolu urobili 5 krokov a nakoniec obaja stoja na rovnakom poli. Ako budeme rozkazovať? Úloha má dve riešenia:
Prvý: "Adam, urob tri kroky vpred, Eva, urob dva kroky vpred, začni hneď!"
Po druhé: "Adam, urob dva kroky späť, Eva, urob tri kroky späť, začni hneď!"
Algebraický zápis problému je: x = y + 1, |x| + |y| = 5 Ak by sme očíslovali bežiaci pás, prešli by sme do ďalšieho prostredia – Schody. Adam stál na kroku 0, Eva na kroku 1. Pri prvom riešení by sa obaja stretli v kroku číslo 3, pri druhom riešení v kroku číslo -2.
Kde alebo ako môžem precvičovať?
Video krokovanie : KROKOVANIE - matematika Hejného metódou - YouTube
Online řešení úloh: Krokování (matika.in)
Online riešenie problémov: Krok (matika.in)
Prostredie
Kamene

V Európe sa rímske číslice používali ešte v 16. storočí predtým, ako Arabi zaviedli indický spôsob písania čísel, ktorý sa ukázal byť výrazne efektívnejší z dvoch dôvodov:
- Bolo možné napísať ľubovoľne veľké číslo pomocou desiatich znakov (číslice 0, 1, 2, ..., 9);
- základné aritmetické operácie (+, -, ·, :) boli oveľa jednoduchšie ako používanie rímskych číslic.
Podstatou indického zápisu čísla je, že rovnaká číslica predstavuje inú hodnotu podľa pozície v čísle. Napríklad číslo 2 v čísle 2 111 predstavuje 2 000, v čísle 1 211 predstavuje 200, v čísle 1 121 predstavuje 20 a v čísle 1 112 predstavuje 2. Žiak v treťom ročníku je už schopný pracovať s trojcifernými číslami, ale neuvedomuje si podstatu pozičného systému. Úlohy z prostredia Kamene sa snažia otvoriť žiakovi prvé pochopenie pozičného systému.
3. a 4. ročník
Najprv sa žiaci oboznámia s naším nástrojom. Čítajú čísla vytvorené kameňmi a používajú kamene na vytvorenie čísel, ktoré hovorí učiteľ alebo spolužiak. Situácia je znázornená na obrázku v úlohe 1.
Úloha 1:

Žiaci majú pripravené pomôcky (napr. pokladničky s tromi priehradkami, papier s daným stolom a pod. a tri predmety – napr. gaštany, viečka, kamene, ...). Potom pomocou tabuľky a troch kameňov tvoria rôzne čísla. Žiaci tak pracujú s vizuálnym znázornením čísla, v ktorom sú zdôraznené poradia čísel. Vytvorením čísla si uvedomia hodnotu na jeho pozícii v zápise. Pracujú teda so zápisom čísla v pozičnej desiatkovej sústave. Hľadaním všetkých riešení sa dostávame do oblasti kombinatoriky a práce s dátami. Žiaci pravdepodobne vyriešia problém náhodným zostavením čísel, niektorí ešte systematickejšie. Ako sa však ubezpečia, že ich zoznam riešení je úplný a že sa neopakuje žiadne číslo? Musia nejako usporiadať množinu čísel. Napríklad podľa veľkosti. Je zaujímavé porovnať rôzne riešenia a opýtať sa, ktorému spôsobu nájdenia všetkých možností žiaci najlepšie rozumejú. Je možné zadať úlohy s väčším počtom kameňov alebo pridať tisíce do tabuľky. Niektorí žiaci zlepšujú svoje výskumné stratégie a volia systematickejšie prístupy. Tieto budú zdieľané s triedou v diskusii.
Úloha 2:
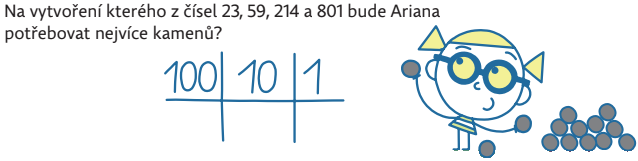
Je veľmi pravdepodobné, že študenti zistia, že počet kameňov na modelovanie čísla je určený súčtom číslic tohto čísla. To otvára myšlienku číselného súčtu, ktorý budeme neskôr potrebovať pre problémy s deliteľnosťou.
Tu môžete vytvoriť ešte sofistikovanejšie úlohy, napríklad: na modelovanie čísla a je potrebných 7 kameňov. Na modelovanie čísla b je potrebných 6 kameňov. Na modelovanie čísla A + B sú potrebné 4 kamene. Nájdite čísla a, b.
Úloha 3:

Pridáme podmienku s číselným súčtom, ale formulujeme ju v prijateľnejšom jazyku. Napriek tomu je úloha na prvý pohľad zložitá. Po vymenovaní všetkých dvojciferných čísel vytvorených pomocou 4 kameňov: 40, 31, 22 a 13 je riešenie zrejmé. Žiaci získajú skúsenosť, že ak úlohu rozdelia na čiastkové kroky, získajú hlbší pohľad na problém. Potom prichádzajú podobné úlohy s väčším počtom kameňov a väčšími rozdielmi.
Úloha 4:

Dalším cílem úloh z prostředí Kameny je připravit žáky na porozumění kritériím dělitelnosti. Cílem uvedené úlohy je jednak mnohé počítání, ale také získávání zkušeností se společnými črty čísel dělitelných třemi. Žáci zjistí, že přidáním jednoho kamene se jim nepodaří vytvořit žádné číslo, které lze dělit třemi beze zbytku (mohou vytvořit čísla 311, 221, 212). Ubráním jednoho kamene mohou vytvořit čísla: 210, 201, 111 a ty lze všechna dělit třemi beze zbytku.
Později přichází úlohy Která trojciferná čísla vymodelována pomocí šesti kamenů jsou dělitelná 3? Která trojciferná čísla vymodelována pomocí devíti kamenů jsou dělitelná 3? a s nimi také další zkušenosti s čísly dělitelnými třemi. Po několika pokusech žáci zjistí, že každé rozložení např. šesti kamenů do tabulky dá číslo dělitelné 3. Třída začne hledat takové rozložení kamenů, aby číslo nebylo dělitelné třemi. Hledání je neúspěšné. V třídní diskuzi postupně zjišťují, že všechna čísla vytvořená ze šesti kamenů jsou dělitelná třemi. Zákonitost objevili, ale její zdůvodnění zatím neznají. To zjistí později, když trojciferné číslo ABC přepíší do tvaru 100A + 10B + C. To se rovná (99A + 9B) + A + B + C. První závorka je jistě dělitelná třemi. Tedy celé číslo je dělitelné třemi, když číslo A + B + C je dělitelné třemi. V našem případě A + B + C je 6 (kamenů). Učitel postupně může měnit počet kamenů, rozšiřovat tabulku o řád tisíců, statisíců apod. Žáci experimentují a když mají dost zkušeností, objeví, že čísla dělitelná třemi jsou ta složená ze 3, 6, 9 atd. kamenů. Tím vlastně objeví a pojmenují kritérium dělitelnosti číslem 3.
5. ročník
Úloha 5:

Pokračujeme v rozšiřování zkušeností potřebných pro vyvození kritérii dělitelnosti i jinými čísly než číslem 3. Žáci zjistí, že třemi jsou dělitelná všechna čísla a dvěma ta, kde na místě jedniček není žádný kámen, 2 kameny nebo 4 kameny.
O niečo neskôr nasleduje analogický problém: Ktoré trojciferné čísla modelované pomocou šiestich kameňov sú deliteľné 6? Ak si študent všimne, že riešenie pre obe úlohy je rovnaké, zdieľa svoje zistenia s triedou.
Úloha 6:

Úlohy sa opakujú v rôznych variáciách, aby študenti mali viac príležitostí získať potrebné skúsenosti na odvodenie pravidiel deliteľnosti alebo na uplatnenie už objaveného pravidla.
Úloha 7:

Cieľom úlohy je získať skúsenosti potrebné na odvodenie kritérií deliteľnosti 9.
Kde alebo ako môžem precvičovať?
My sme použili prostredie kamene na zápis čísla v desiatkovej sústave
Video: Rozklad čísla v desiatkovej sústave - YouTube
Pomôcka na doma: vyrob si tabuľku na výkres podobnú tejto a podľa návodu z hodiny môžeš použiť na miesto kameňov fazuľky alebo hrach alebo korálky
|
1
|
10
|
100
|
1000
|
10000
|
100000
|
1000000
|
10000000
|
100000000
|
1000000000
|
|
........
|
|
|
|
|
...
|
..
|
|
|
|
Príklad : Zapíš číslo 2 300 008 v desiatkovej sústave.
Najprv si vyjadri číslo pomocou kameňov do tabuľky ako na obrázku.
Následne zapíš matematickým zápisom.
- 300 008= 2.1000000+3.100000+8.1
Príklady na precvičenie:
Urči počet jednotiek, desiatok, stoviek, atď. Vyplň tabuľku.
|
|
|
|
|
|
|
|
|
|
|
|
|
3 879 031 165
|
|
|
|
|
|
|
|
|
|
|
|
76 421 980
|
|
|
|
|
|
|
|
|
|
|
|
987 432 006
|
|
|
|
|
|
|
|
|
|
|
|
2 504 034 698
|
|
|
|
|
|
|
|
|
|
|
|
65 450 219
|
|
|
|
|
|
|
|
|
|
|
|
842 105
|
|
|
|
|
|
|
|
|
|
|
|
9 453 219 507
|
|
|
|
|
|
|
|
|
|
|
Prostredie
Číselná os
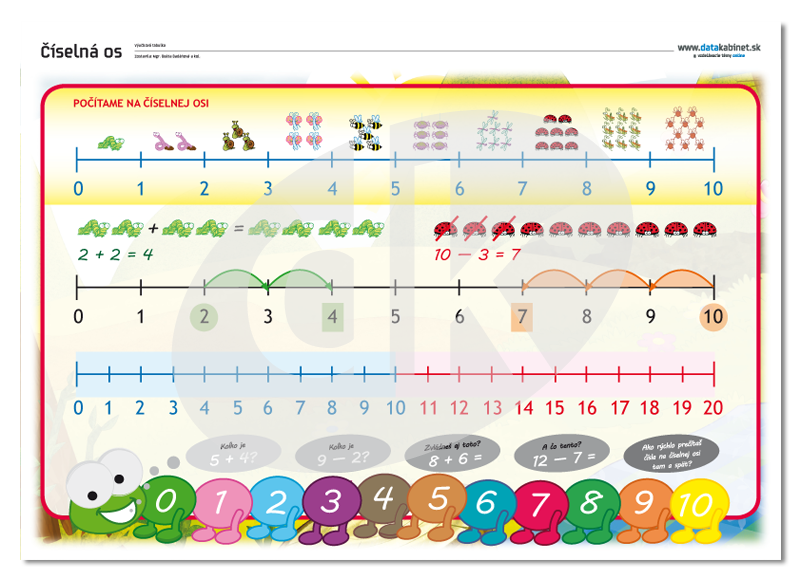
Žiak zažíva svoje prvé stretnutie s číselnou osou v prostredí schodov.
Žiaci riešia veľa problémov pohybom po číselnej osi, ale nazývajú to šliapaním po schodoch alebo na bežiacom páse s číslami. Týmto skúsenostiam predchádza mnoho skúseností získaných z riešenia úloh v Steppingu, a teda na bežiacom páse bez čísel.
1. ročník
Úloha 1:

Žiak zažíva svoje prvé stretnutie s číselnou osou v prostredí schodov. Obrázok ukazuje schody a po splnení úloh na skutočných schodoch ich žiaci modelujú v triede ako odrazový pás s číslami.
Žiaci riešia veľa problémov pohybom po číselnej osi, ale nazývajú to šliapaním po schodoch alebo na bežiacom páse s číslami. Týmto skúsenostiam predchádza mnoho skúseností získaných z riešenia úloh v Steppingu, a teda na bežiacom páse bez čísel.
Úloha 2:
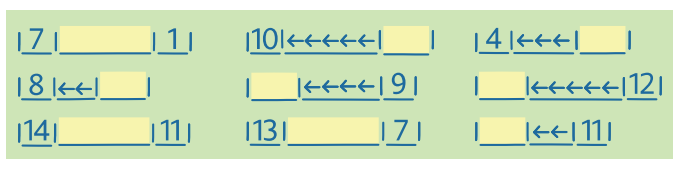
V prostredí Schody sa riešia náročnejšie úlohy, ktoré dávajú deťom dobrú skúsenosť, ktorú môžu využiť pri práci s číselnou osou. V 1. ročníku uprednostňujeme tento variant (sémantizovanej) číselnej osi, to znamená, že čísla vyjadrujú "meno" / "adresu" kroku. Okrem toho žiaci získavajú skúsenosti prostredníctvom skúseností, t. j. pohybom vlastného tela.
Žiaci sa stretávajú s obvyklou formou číselnej osi, kde sú čísla už abstraktné, až v 2. ročníku.
2. ročník
Úloha 3:


V týchto úlohách žiaci absolvujú číselný rad a uvedomia si jeho lineárne usporiadanie a rovnakú vzdialenosť medzi susednými číslami. Čísla sú v abstraktnej forme, ale keď študent poukáže na to, že je to rovnaké ako schody, učiteľ túto myšlienku podporuje. To je dôležité pre vytvorenie sémantickej myšlienky abstraktného konceptu, ktorý je predpokladom dobrého porozumenia.
Úloha 4:
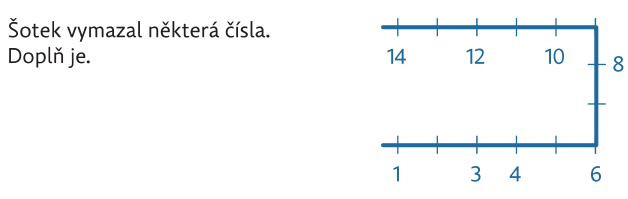
Táto úloha búra predsudky, že číselná os musí ísť iba zľava doprava.
Aj v 2. ročníku žiaci riešia veľké množstvo úloh v prostredí Stupňovanie a Schodiská.
Úloha 5:
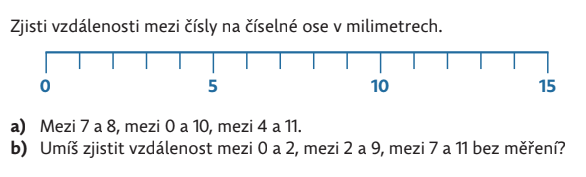
Číselná os sa používa aj na meranie v milimetroch. Aby žiaci zistili vzdialenosti medzi číslami, je potrebné merať aspoň raz.
Žiaci môžu označiť všetky čísla na číselnej osi a zmerať požadované vzdialenosti. Je však výhodnejšie zmerať vzdialenosť dvoch susedných čísel (1 delenie) a potom vynásobiť príslušným číslom. Žiaci tak získavajú skúsenosti s priamou proporcionalitou. Z poznania dĺžky jedného kusu vypočítajú dĺžku napríklad siedmich kusov.
Úloha 6:

Ďalej sa číselná os používa na otvorenie myšlienky zaokrúhľovania. Rozdiel dvoch čísel je vizualizovaný vzdialenosťou dvoch bodov. Silne označené sú tie čísla, vzhľadom na ktoré budú čísla zaokrúhlené. Napríklad číslo 12 je bližšie k 10 ako 20, takže 12 bude zaokrúhlené na 10.
Úloha 7:

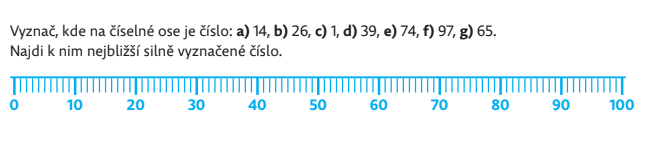
Naďalej otvárame myšlienku zaokrúhľovania čísel. Pásmový meter (napr. papier, skladanie, rolovanie) slúži ako vhodná pomôcka pri tejto činnosti.
Vo všetkých úlohách okrem poslednej je výsledok jednoznačný. O čísle 65 sa bude pravdepodobne diskutovať. Táto úloha má dve možné riešenia – číslo 60 a číslo 70. Z matematického hľadiska sú obe riešenia rovnaké, ani jedno nemožno uprednostniť. Zatiaľ necháme obe možnosti v hre, ale o niečo neskôr uzavrieme dohodu, ktorá sa bude zaoberať týmito dvoma možnosťami. Táto zmluva znie: Číslo, ktoré končí číslom 5, sa zaokrúhli nahor. Napríklad číslo 135 sa zaokrúhľuje na desiatky až 140.
Úloha 8:
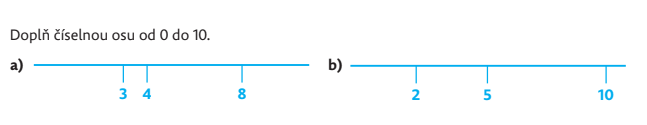
Žiak môže použiť merania alebo označiť vzdialenosť medzi dvoma číslami, najlepšie susednými číslami, na kúsku papiera. Potom prenáša túto vzdialenosť. V úlohe b) má žiak viac možností, preto je užitočné hľadať viac spôsobov riešenia. Napríklad môže použiť vzdialenosť medzi 5 a 10, z ktorých nájde 0, od 0 a 2 nájde 4 a má dve po sebe idúce čísla 4 a 5. Alebo použije vzdialenosť medzi 2 a 5, z ktorých nájde 8 a potom z 10 nájde 7 a už má po sebe idúce čísla 7 a 8.
Zobraziť riešenia
4. ročník
Úloha 9:
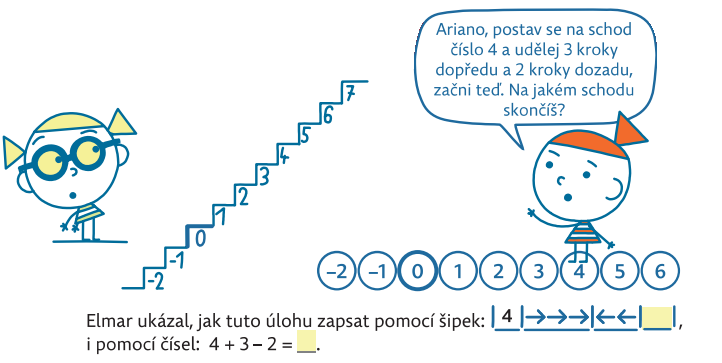
Při otevírání kognitivně náročnější látky, což jsou záporná čísla, se vracíme do sémantiky, tj. do krokování na schodech. Tímto způsobem se rozšiřuje i číselná osa o záporná čísla, jak je vidět v následující úloze.
Úloha 10:
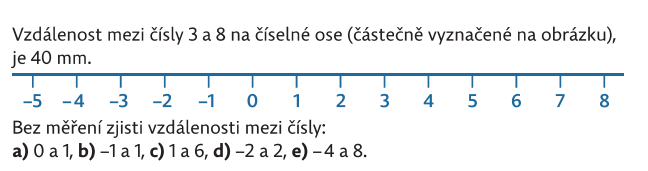
Porozumění práci na číselné ose podporuje průběžné řešení velkého množství úloh v prostředí Krokování a Schodů.
Číselná osa je významnou pomůckou pro řešení úloh o věku. Např. Aničce jsou 3 roky. Až jí bude tolik, kolik je Honzíkovi, Honzíkovi bude 11 let. Kolik je dnes Honzíkovi.
Zobraziť riešenia
5. ročník
Úloha 11:
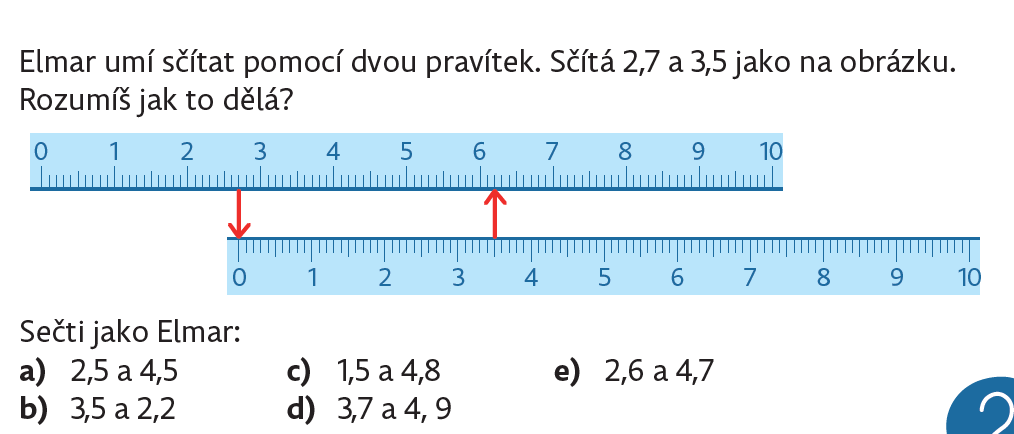
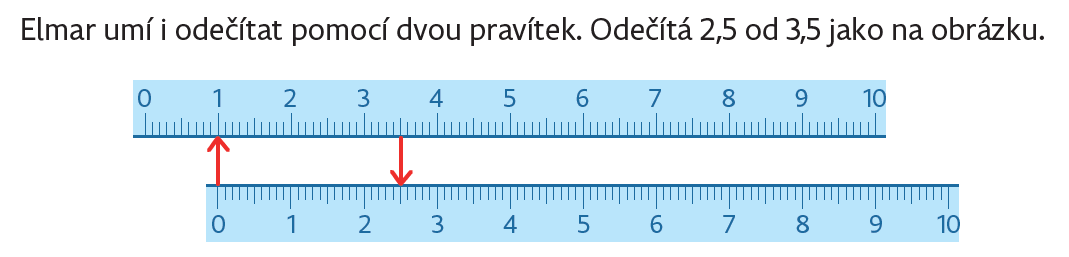
Číselnú os, ktorá môže byť tiež reprezentovaná mierkou, možno použiť na sčítanie a odčítanie dvoch čísel, dokonca aj desatinných. Sčítanie/odčítanie je modelované ako grafický súčet/rozdiel dvoch čiar.
Práca na číselnej osi spolu s krokom pomáha pochopiť úlohy v prostredí mriežky, napr. pri odvodzovaní a práci so súradnicami bodov mriežky.
Kde alebo ako môžem precvičovať?
My sme použili prostredie číselná os na zavedenie celých čísel , na zaokrúhľovanie , na sčitovanie, odčitovanie, násobenie, delenie ale aj na predstavu o zlomkoch a iné
Naučili sme sa
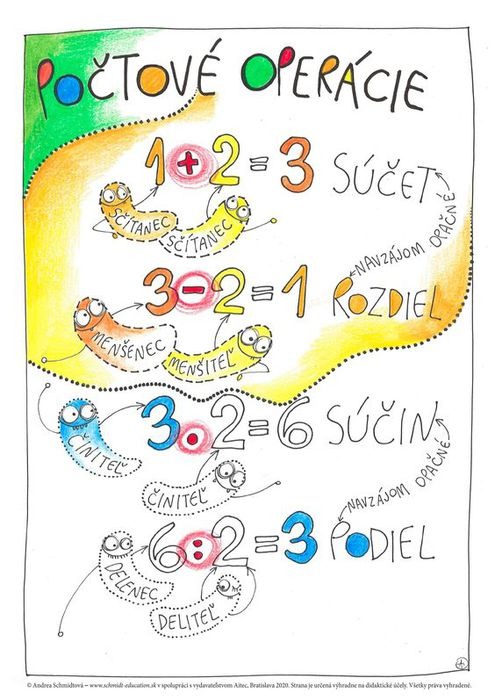
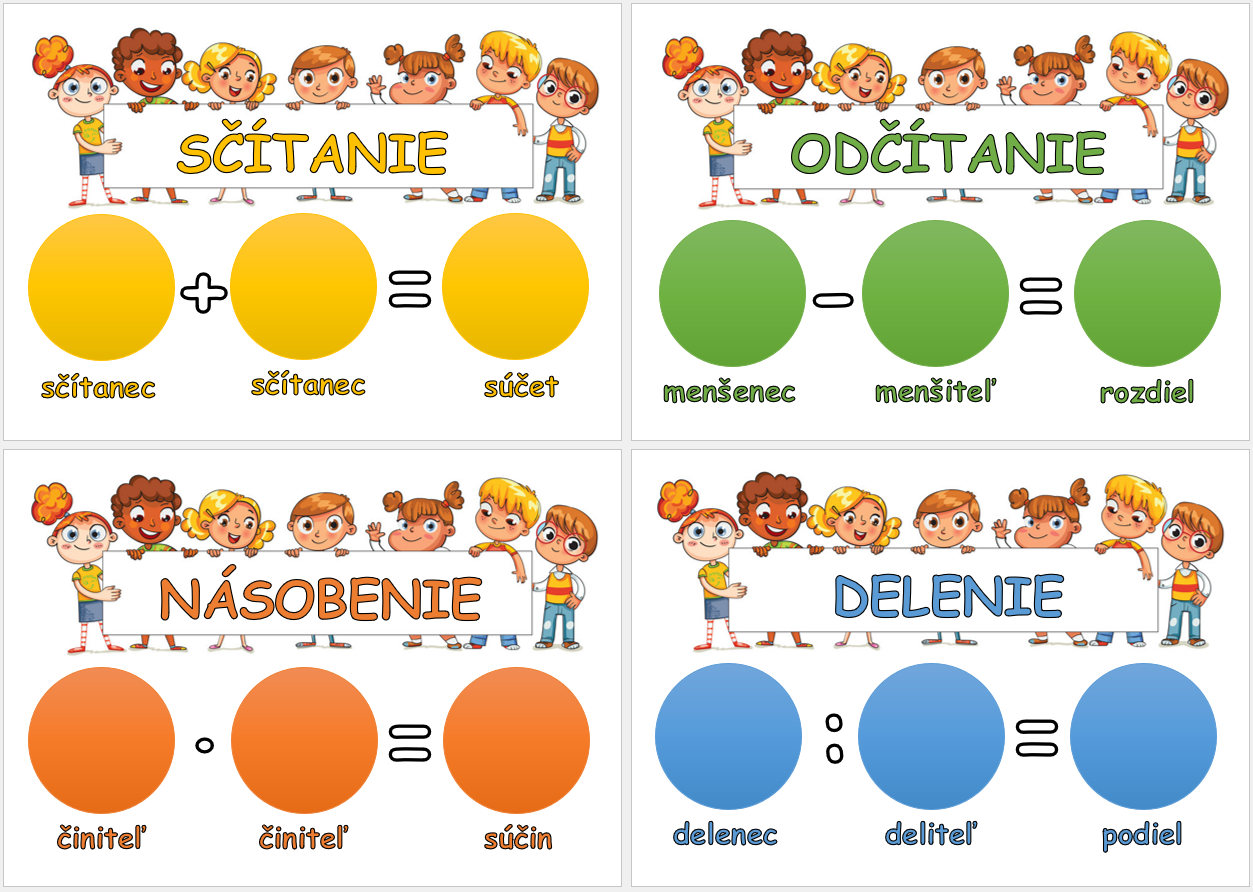

Prostredie:
ABAKU
Hlavným cieľom prostredia Abaku je posilniť číselné (výpočtové) spojenia. Ide o spojenia typu 2 + 3 = 5, 4 + 6 = 10, násobiace spojenia atď. Ak žiak Vytvorí také kĺby, v budúcnosti mu to uľahčí prácu témy matematiky – napr. v rozširovaní a skrátení zlomkov. Je dôležité, aby Žiaci robili takéto školenie so záujmom, aby to necítili ako nudné, aby Bavil.
Abaku
Prostredie Abaku je jedným z nových prostredí Hejného metódy. Vznikla vďaka prepojeniu s tímom Abaku (pani učiteľka Alena Vávrová a spol.), ktorý sa okrem metodiky zaoberá aj stolovou hrou Abaku (aj v online verzii). Viac informácií, pomôcok a elektronickú prihlášku Abaku nájdete na ich webových stránkach abaku.org. Aj keď sa naše nové prostredie líši v určitých pravidlách s Abaku, vo väčšine prípadov je to rovnaké. Okrem hlavného cieľa posilnenia výpočtových spojení sa chceme zamerať na ďalšie oblasti matematiky v životnom prostredí: ekvivalentnú modifikáciu rovníc, kombinatoriku, paritu (rovnomernosť, lichotenie) atď.
1. ročník

Prostredie vstupuje do učebníc na konci 1. ročníka. Úlohou žiakov je nájsť pravidlo, podľa ktorého čísla bývajú v byte a pripočítať čísla pred bytovým domom k voľným bytom. Viete nájsť pravidlo?
Pravdepodobne ste nemali problém zistiť, že ak sčítate dve čísla, dostaneme tretie číslo. Matematici tu hovoria o numerickej triáde a + b = c. Žiaci sa učia vidieť súvislosti ako 3 + 4 = 7, 2 + 5 = 7 atď.
Ich úlohou je ospravedlniť každú trojicu, napr. v ľavom hornom byte 6 = 5 + 1. Postupom času sa v triede 6 - 5 = 1 objaví ďalšie odôvodnenie. Vzhľadom na to, že poradie čísel v bytoch nie je pevne stanovené (žiaci si ich môžu ľubovoľne vymieňať), žiaci pracujú s dôležitými vzťahmi a + b = c → a = c – b alebo b = c – a.
V ďalšej úlohe majú žiaci možnosť splniť svoje trojčatá v posledných dvoch úlohách. To môže byť diagnostické pre učiteľov aj rodičov. Žiaci často vypĺňajú veľké počty, napr. 100, 100, 200. To ukazuje ich fascináciu a potrebu pracovať s takýmito číslami.

Ak sa neobjavilo viacciferné číslo, študenti ho dokončia v nasledujúcej úlohe s 9 a 6: problém má dve riešenia 3 alebo 15. V pilotných triedach žiaci uprednostňovali číslo 15 viac, pretože bolo pre nich prirodzenejšie pridávať pridelené čísla.

Doteraz mali žiaci slobodu vo vytváraní triád (trojíc). To znamená, že pri vytváraní rovnosti mohli ľubovoľne vymieňať čísla, napr. z čísel 3 6 9 mohli písať rovnosť v rôznych postupnostiach čísel: 3 + 6 = 9, 9 - 6 = 3, 9 = 6 + 3, 6 = 9 - 3 atď. V ďalšej úlohe sú čísla pevné.

Zafixování čísel je motivováno povídáním o vizitkách na zvoncích paneláku. Stejně jako v běžném životě nelze změnit pořadí příjmení Novák na např. Vánok, tak nelze měnit zadanou vizitku čísel. Čísla jsou napsána v pevném pořadí. Úkolem žáků je vložit mezi čísla rovnítko a početní operaci, aby byla rovnost pravdivá.
2. ročník
Úloha 1:

Jedná se o kombinatorickou úlohu, žáci zjišťují, jaké různé vizitky ze tří čísel lze vytvořit. Nebo-li jaké pořadí lze z daných tří čísel vytvořit, abychom vložením znaménka početní operace a rovnítka získali rovnost.
Úloha 2:

Zatím se v úlohách objevovalo sčítání a odčítání. V posledních dvou vizitkách se nyní objevuje příležitost k použití násobilky. Je to v době, kdy do učebnic přichází zavedení násobilky. Navíc, více žáků již často o násobilce ví z domova nebo od spolužáků.
Do abaku úloh vstupuje násobilka. Žáci opět toto pravidlo mají najít.

Stejně jako u sčítání žáci mají volnost k tvorbě úloh (pořadí číslic není fixováno). U levého horního bytu tak mohou vytvořit rovnosti jako . Tím žáci získávají zkušenosti s komutativitou násobení (). Najde se možná i žák, který navrhne zdůvodnění . Ve třídě učitel musí zvážit z reakcí žáků, jestli s tím má smysl pracovat nebo dělení odložit až na později, kdy bude operace zavedena.
Typologie úloh je stejná jako u úloh se sčítáním a odčítáním. V další úloze žáci zjišťují, zda se jedná o násobilkovou trojici.
Úloha 3:

Úloha 4:

Poté následují vizitky, kterými se opět fixuje pořadí čísel. Žáci tedy vkládají mezi čísla = a početní operaci, aby platila rovnost. První sloupec je na sčítání a odčítání, druhý na násobení (případně dělení).
Úloha 5:

Při doplňování vizitek učitel může sledovat, zda žáci preferují sčítání (odčítání) nebo násobení (dělení).
Úloha 6:

Zobraziť riešenia
3. ročník
Do mesta Abaku prichádza nová vec – poznávacia značka Abaku. Na rozdiel od vizitiek sú 4 číslice pevné. Kombináciou dvoch číslic je možné vytvoriť dvojciferné čísla.
Cieľ problémov inak zostáva rovnaký, nahradiť = aritmetickú operáciu medzi danými číslami tak, aby sa vytvorila rovnosť.
Poznávacie značky sú motivované rovnakými úlohami od už spomínanej Mgr. Aleny Vávrovej. V jej triedach boli úlohy také populárne, že žiaci z vlastnej iniciatívy hľadali vizitky Abaku na autách v každodennom živote. Odfotografovali ich a vytvorili nástenku so "správnymi" poznávacími značkami. To tiež zlepšilo ich číselné pripojenie. V ideálnom prípade sa žiak zlepšuje, ak úlohy rieši vlastnou vnútornou motiváciou.

Po poznávacích značkách Abaku prichádzajú reťaze Abaku. Tieto už nie sú obmedzené počtom číslic. Žiaci hľadajú všetku rovnosť, dokonca aj čiastočnú. Preto už nie je potrebné vytvárať rovnosť so všetkými zadanými číslicami. Je to vidieť na obrázku 4, 3, 1, 2, jedna z rovnosti, i 3 – 1 = 2.

Postupne sa reťazce skladajú z viacerých čísel a úlohou je nájsť čo najviac rovnosti. Je pravda, že vždy sa používa jedno znamienko rovnosti a jedna aritmetická operácia. Čísla môžu byť cielene zvolené tak, aby vytvorili zdanlivo skryté riešenia – napr. v poslednom reťazci je možné vytvoriť rovnosť 15 = 69 – 54. Tieto úlohy sú medzi žiakmi obľúbené, učia sa číselné spojenia a bavia sa tým.
Pokúsite sa nájsť všetky riešenia v troch reťazcoch?
Úloha 7:






















 Sčitovanie a odčitovanie
Sčitovanie a odčitovanie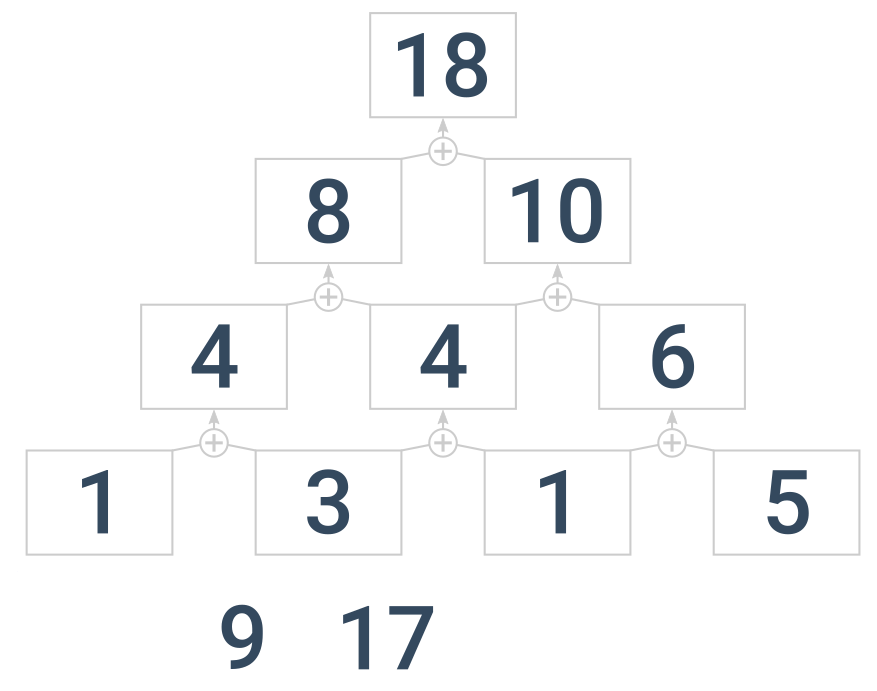
















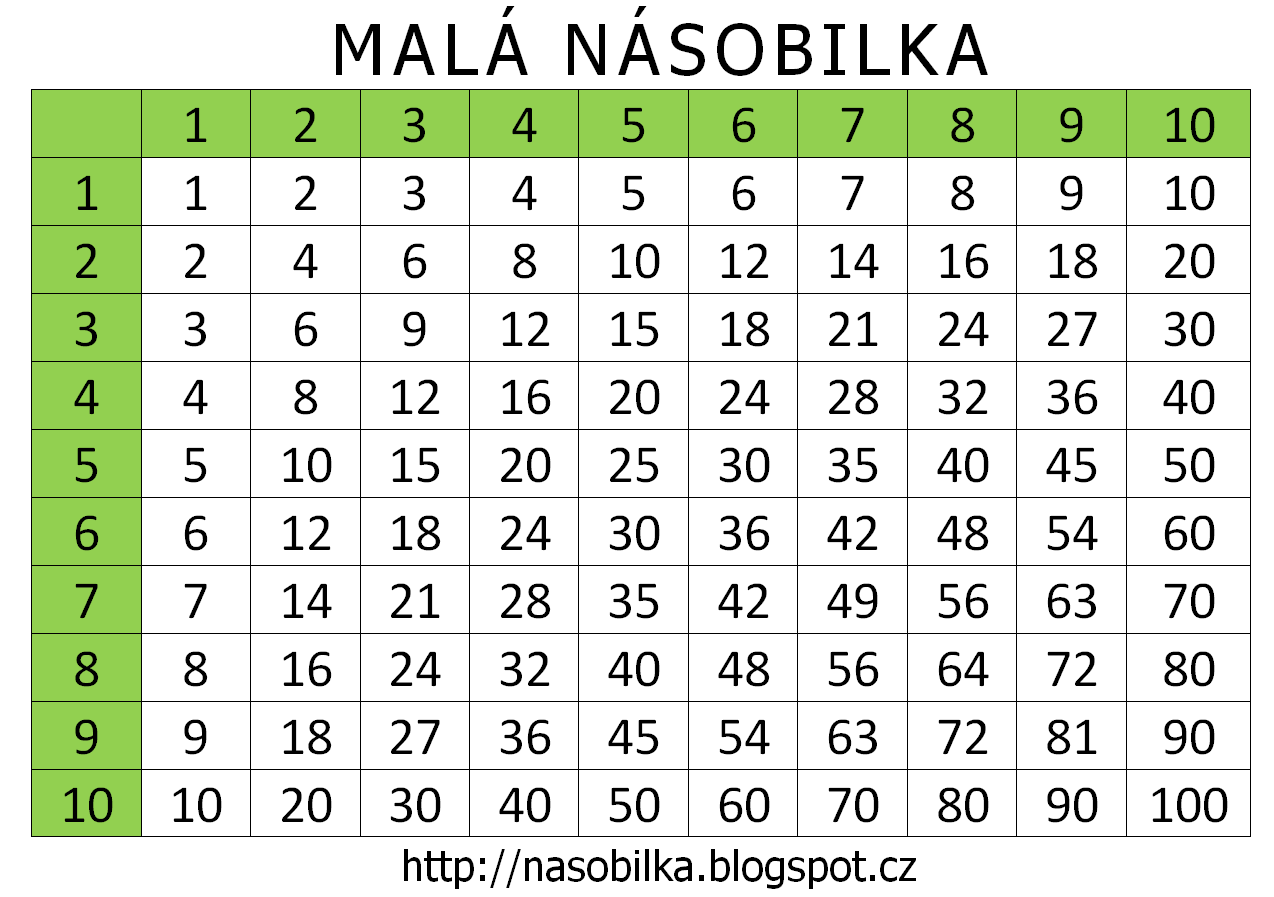



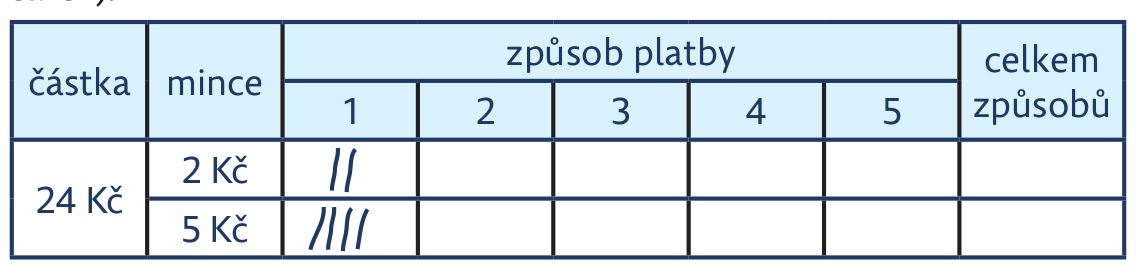

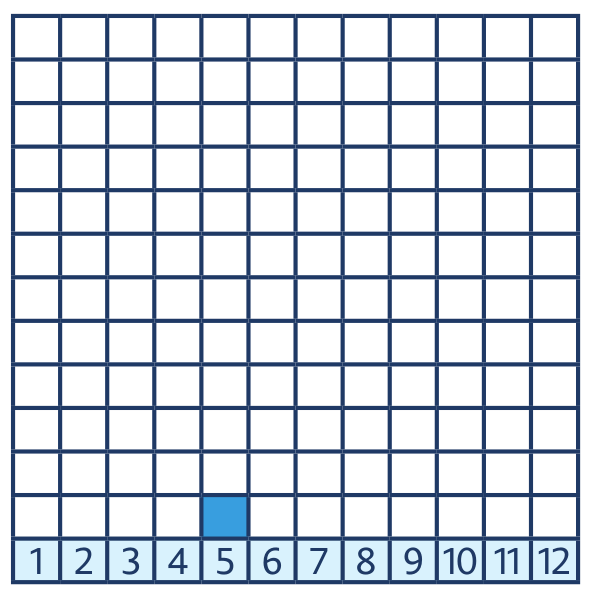
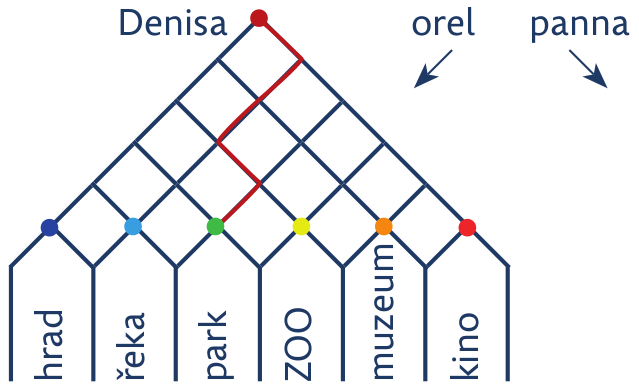


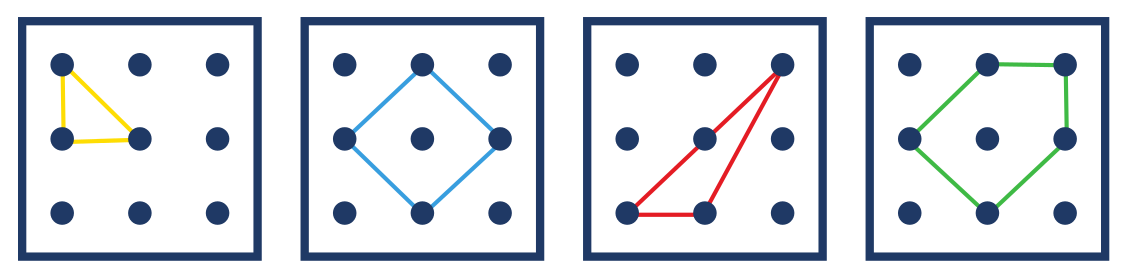



 . Obsah červeného trojúhelníku je jeden kachlík.
. Obsah červeného trojúhelníku je jeden kachlík.